Year 2: Issue #3 - Feb 20, 2022

This journal issue includes problems from our collaboration with the students at Upper School in Bucharest, Romania. The students’ submissions were coordinated by Prof. Mihaela Berindeanu.

Problems A (Not open to Grade 11 and 12 students)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Sunday, April 10, 2022 to submit solutions.

Problem 35A. Proposed by DC
In trapezoid $ABCD$, the bases are $AB$=7 cm and $CD$=3 cm. The circle with the origin at $A$ and radius $AD$ intersects diagonal $AC$ at $M$ and $N$. Calculate the value of the product $CM \times CN$.

Problem 67A. Proposed by Eliza Andreea Radu
Consider the convex quadrilateral $ABCD$ and the parallelograms $ACPD$ and $ABDQ$. Find $m(\measuredangle (AC, BD))$ knowing that $BP=16$, $CQ=12$, $AC=4$, and $BD=7\sqrt{2}$.

Problem 76A. Proposed by Vedaant Srivastava
Find all triples $(x, y, z) \in \mathbb{R}^3$ that satisfy the following system of equations: \[ \begin{cases} x^3 = -3x^2-11y+26\\ y^3 = 3y - 7z + 23\\ z^3 = -9z^2 + 13x - 121 \end{cases} \]

Problem 78A. Proposed by Aurelia Georgescu
Find $x$, $y \in \mathbb{Z}$ such that $\frac{4x^2+10x+7}{4y^3-12y^2+8y-1} \in \mathbb{Z}$.

Problem 86A. Proposed by Maria Radu
Find how many values $n \in \mathbb{R}\setminus \mathbb{Q}$ satisfy the condition that both $4n^2-6n-2$ and $4n^3-2n^2-1$ are simultaneously rational numbers.

Problem 88A. Proposed by Nicholas Edmond Teler
Solve in $\mathbb{Z}$ the equation: \[(36x^2+204x+289)(3x+11)(x+2)=-2028\]

Problem 89A. Proposed by Vlad Armeanu
Solve in $\mathbb{R^{+}}$ the system of equations: \[ \begin{cases} a\cdot b \cdot c =125\\ (a+b+c)^3(\frac{1}{a^3+1000}+\frac{1}{b^3+1000}+\frac{1}{c^3+1000})\leq 9 \end{cases} \]

Problem 90A. Proposed by Matei Gheamalinga
Solve for $x$ and $y$ in $\mathbb{Z}$ the system of equations: \[ \begin{cases} 9x^2+x^2y^2-6y =0\\ x^5+4y^2-16y+17=0 \end{cases} \]

Problem 91A. Proposed by Vlad Armeanu
Solve in $\mathbb{R}$ the system of equations: \[\left\{ \begin{array}{l} 5^{x} +3^{x}= 6y+2 \\ 5^{y}+3^{y}=6z+2\\5^{z}+3^{z}=6x+2\\ \end{array} \right. \]

Problem 92A. Proposed by Denisa Dragomir
Solve in $\mathbb{R}$ the equation: \[\left [\frac{x^2+2x+3}{x^2+2}\right] = \sqrt{x-2\sqrt{x-1}} \]

Problem 93A. Proposed by Luca Vlad Andrei
If $a,b,c,d \in [0,1]$, prove that : $$\frac{a+b+c}{8085+b^{2022}+c^{2022}+d^{2022}}+ \frac{a+b+d}{8085+a^{2022}+b^{2022}+c^{2022}}+$$ $$+\frac{a+c+d}{8085+a^{2022}+b^{2022}+d^{2022}}+\frac{b+c+d}{8085+a^{2022}+c^{2022}+d^{2022}}\leq \frac{3}{2022}$$

Problem 94A. Proposed by Luca Vlad Andrei
Find $a, b, c >0$ satisfying both conditions: $$a^2+b^2+c^2 >0$$ and $$(16a^3+256a-68)(2b^3+8b+31)(6c^3+54c+162)\geq 9^3(a^2+94)(b^2+10)(c^2+45).$$

Problem 95A. Proposed by Matei Neacsu
Solve in $x,y,z\in\mathbb{R^*}$ the system: $\left\lbrace\begin{array}{l} x+11=\dfrac {y-25}{x}\\ y+11=\dfrac{z-25}{y}\\ z+11=\dfrac{x-25}{z} \end{array}\right.$

Problem 96A. Proposed by Iancu-Ioan Sandea
Find the positive real numbers $x,y,z$ satisfying both conditions: $x+y+z=21$ and $\sqrt{21x+yz}+ \sqrt{21y+xz}+\sqrt{21z+xy} \geq 42$.

Problem 97A. Proposed by Nicholas Edmond Teler
If $4\mid y$ and $2^{4x-5}+2^{4y+3} \leq 2^{2x+2y}$, find the last digit of the number $2^{2x}+2^{2y}$.

Problem 98A. Proposed by Teodor Melega
Triangle $ABC$ has point $H$ as its orthocenter. Let $D$ be the intersection of line $AH$ and the tangent that touches the circumcircle of triangle $ABC$ at $B$. Line $DB$ intersects the circumcircle of triangle $AHB$ at a second point, $X$. Line $DC$ intersects the circumcircle of triangle $AHC$ at a second point, $Y$. Prove that the intersection point of $XY$ and $AB$ lies on the circumcircle of triangle $AHC$.

Problem 99A. Proposed by Iancu-Ioan Sandea
Positive real numbers $a,b,c$ satisfy the condition that $a+b+c=15$. Find the minimum of $E=100(\frac{a}{15-a}+\frac{b}{15-b}+\frac{c}{15-c})-a^2-b^2-c^2+2581$ and the values of $a,b,$ and $c$ that result in this minimum.

 

Problems B (Open to all Grades)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on April 10, 2022 to submit solutions.

Problem 39B. Proposed by Alexander Monteith-Pistor
For $n \in \mathbb{N}$, let $S(n)$ and $P(n)$ denote the sum and product of the digits of $n$ (respectively). For how many $k \in \mathbb{N}$ do there exist positive integers $n_1, ..., n_k$ satisfying $$\sum_{i=1}^k n_i = 2021$$ $$\sum_{i=1}^k S(n_i) = \sum_{i=1}^k P(n_i)$$

Problem 40B. Proposed by Vedaant Srivastava
Two identical rows of numbers are written on a chalkboard, each comprised of the natural numbers from 1 to $10!$ inclusive. Determine the number of ways to pick one number from each row such that the product of the two numbers is divisible by $10!$

Problem 56B. Proposed by Alexander Monteith-Pistor
A game is played with white and black pieces and a chessboard ($8$ by $8$). There is an unlimited number of identical black pieces and identical white pieces. To obtain a starting position, any number of black pieces are placed on one half of the board and any number of white pieces are placed on the other half (at most one piece per square). A piece is called matched if its color is the same of the square it is on. If a piece is not matched then it is mismatched. How many starting positions satisfy the following condition $$ # of matched pieces -# of mismatched pieces = 16$$ (your answer should be a binomial coefficient).

Problem 67B. Proposed by Stefan-Ionel Dumitrescu
Consider a cube $ABCDA'B'C'D'$. Point $W$ can be in the interior, on the faces, or on the edges of the cube. Point $X$ can be in the interior of the cube or on the edges of face $ADD'A'$. Point $Y$ can be in the interior of the cube or on the edges of face $ABB'A'$. If $Z$ is the midpoint of $XY$, what is the probability of finding a pair of points ($X$,$Y$), where $W$ is the midpoint of $AZ$?

Problem 76B. Proposed by Alexander Monteith-Pistor
Let $ABCD$ be a quadrilateral with $\measuredangle ABC = 90^{\circ}$. Points $E$ and $F$ are on $AD$ and $BC$ respectively such that $AB$ is parallel to $EF$. Further, $AC, BD$ and $EF$ intersect at $O$. Given that $BF = 4$, $AB = 9$, $AE = 5$ and $CD = 20$, find a polynomial $p(x)$ such that one of its roots is at $x = \frac{DO}{OB}$.

Problem 77B. Proposed by Andy Kim
(i) Evaluate $${n \choose 0} - 2 {n \choose 1} + \dots \pm 2^n {n \choose n} = \sum_{i=0}^{n} (-1)^i 2^i {n \choose i}$$ for $n\in \mathbb{Z_{+}}$.
(ii) Prove that $$\sum_{i=0}^{n} (-1)^{n-i} i^n {n \choose i} = n!$$ for all $n\in \mathbb{Z_{+}}$.

Problem 78B. Proposed by Pavel Ciurea
Given the positive real numbers $x$, $y$, and $z$, prove that $$2(\sum_{cyc}x) \sqrt{\sum_{cyc}\sqrt{x^2+y^2+z^2}}\geq$$ $$\geq \sum_{cyc} \sqrt{3(x+y)(x+z)(\sqrt{x^2+y^2+xy}+\sqrt{x^2+z^2+xz}-\sqrt{y^2+z^2+yz})}.$$

Problem 80B. Proposed by Pavel Ciurea
Given the positive real numbers $x,y,z$ and $t$, prove that: $$\frac{2xy}{yt}+\frac{2yt}{xz}+\frac{y}{z}+\frac{z}{y}+2\sqrt{(\frac{x}{y}+\frac{y}{x})(\frac{z}{t}+\frac{t}{z})(\frac{y}{z}+\frac{z}{y}-1)(\frac{x}{t}+\frac{t}{x}+1)}\geq $$ $$ \geq \frac{x}{t}+\frac{t}{x}+\sqrt{3}(\frac{x}{z}+\frac{z}{x}+\frac{y}{t}+\frac{t}{y})+4.$$

Problem 81B. Proposed by Alexandru Benescu
Let $ABC$ be a triangle, $H$ its orthocenter and $X,Y,Z$ the circumscribed circles of $\Delta BHC$, $\Delta AHC$, and $\Delta AHB$ respectively. Let $DE$ be the common tangent to $X$ and $Y$, $EF$ to $Y$ and $Z$, and $FD$ to $X$ and $Z$, such that all three circles $X,Y,Z$ are inside $\Delta DEF$. Prove that $AD$, $BE$ and $CF$ are concurrent.

Problem 82B. Proposed by Alexandru Benescu
Prove that: $$(a+b+c+2)^2+\frac{5}{2}(a+b)(b+c)(c+a)+2(a^3+2)(b^3+2)(c^3+2)+1 \geq 100abc$$ where $a$, $b$, $c \in \mathbb{R_{+}}$ and $a^2+b^2+c^2=3$.

Problem 86B. Proposed by Nicholas Sullivan
Suppose there are 2021 people sitting at a very large circular table. How many ways are there to give each person a red, blue or green hat such that no two neighbouring people have the same colour hat?

Problem 87B. Proposed by Max Jiang
There is a row of $n$ pies, numbered 1 to $n$ from left to right. You start at pie 1 and go rightward. At each pie, there is a $1/2$ chance that you eat the pie, after which you move on to the next uneaten pie (which depends on the direction you are moving). Upon reaching the last uneaten pie, you change the direction you are going (if the last pie still uneaten you will "repeat" it). You continue until all pies are eaten. What is the probability that pie 1 is the last pie you eat? Express your answer as a finite sum in terms of $n$.

Problem 88B. Proposed by Daisy Sheng
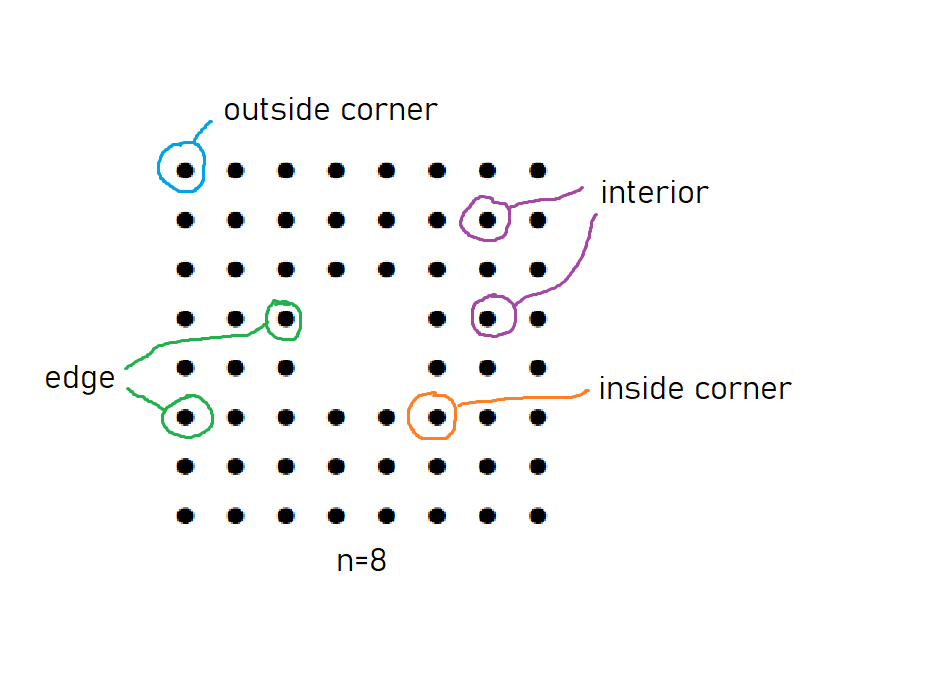
Pierre is coloring a $n\times n$ square grid, where $n$ is even and $n\geq 8$. He chooses to omit the centre $2 \times 2$ square grid (see diagram for an example). In the spirit of the holidays, Pierre is coloring the dots either red or green. He also connects horizontally, vertically, and diagonally adjacent dots with lines using the following color scheme rules:
- 2 red dots are connected by a gold line segment;
- 2 green dots are connected by a blue line segment;
- a red and green dot are connected by a silver line segment.
Let there be: $r_0$ red outside corner dots, $r_1$ red inside corner dots, $r_2$ red edge dots, and $r_3$ red interior dots. If $B$ is the overall number of blue line segments and $G$ is the overall number of gold line segments, find $G$ in terms of $B, n, r_0, r_1, r_2,$ and $r_3$.


Problem 89B. Proposed by Arnab Sanyal
Let $\omega_1$ and $\omega_2$ be two intersecting circles. Let $\omega_1 \cap \omega_2= \{P,Q\}$. Let the tangent to $\omega_1$ and $\omega_2$ at $P$ meet $\omega_1$ and $\omega_2$ respectively at $B$ and $A$. Let the circumcircle of $\Delta PBA$ be $\omega_0$. $AQ$ meets $\omega_0$ (possibly extended) at $Y$ and $BQ$ meets $\omega_0$ (possibly extended) at $X$. Assuming $P \neq Q$, prove or disprove the following statements:
(i) $XABY$ is an isosceles trapezoid;
(ii) $QOBA$ is cyclic, where $O$ is the circumcenter of $\omega_0$.

Problem 90B. Proposed by Gabriel Crisan
If $a,b,c\in \mathbb{R}$, prove that : $$\frac{1}{2^{a-b+3}+1}+\frac{1}{2^{b-c+3}+1}+\frac{1}{2^{c-a+3}+1} \geq \frac{1}{3}$$

Problem 91B. Proposed by Stefan Ionel Dumitrescu
Let $n,m$ be natural numbers, where $n \geq 3$, $m \geq 2$, and $n > m$. Let's define a table of real numbers with $m$ rows and $n$ columns: $$T = \begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{pmatrix}$$ This table has the property that the sum of the squares of the numbers in each column is $1$, namely: $$a_{1i}^2 + \dots + a_{mi}^2 = 1, (\forall) \ i \in \overline{1, n}$$ For each line, we define a variable $A_j$ that represents the sum of all the pairwise products of the $n$ numbers appearing in that row, meaning that: $$A_j = a_{j1}a_{j2} + a_{j1}a_{j3} + \dots + a_{j(n - 1)}a_{jn}, (\forall) \ j \in \overline{1, m}$$ Prove that: $$\sum_{i = 1}^{m} A_i < \frac{n^n}{4(n - 2)^{n - 2}}$$

Problem 92B. Proposed by Gabriel Crisan
If $a,b,c\in \mathbb{R^{+}}$ and $\log_ab \cdot \log_bc \cdot \log_ca =1$, prove that : $$\frac{1}{\log_aab^7}+\frac{1}{\log_bbc^7}+\frac{1}{\log_cca^7} \geq \frac{3}{8}$$

Problem 93B. Proposed by Radu Stoleru
Triangle $ABC$ has all interior angles less than 75 degrees. Find the point $M$ in interior of the triangle such that $MA \cdot \frac{1+\sqrt{3}}{\sqrt{2}} + MC \cdot \sqrt{2}+MC$ is minimum.

Problem 94B. Proposed by Iulia Slanina
Let $(x_n)$ be a sequence in $\mathbb{R^{+}}$ such that $x_1=\frac{1}{16}$ and $x_{n+1}=16x_n^3$. Let $(y_n)$ be a sequence in $\mathbb{R^{+}}$ such that $y_n=16x_n^2+4x_n+1$.
Find $\lim_{n\rightarrow \infty}(y_1y_2\cdots y_n)$.

Problem 95B. Proposed by Daisy Sheng
Prove that $$6n + \prod_{k=0}^{2n-1}\frac{k^3+2k^2+2k+1}{k^3-(2n+1)k^2+(2n+1)k-2n}$$ is an odd perfect square for all $n\in \mathbb{Z}^+.$

Problem 96B. Proposed by Vedaant Srivastava
Arrange the numbers from 1 to 2022 in a circle. Label the numbers $(x_1, x_2, \dots, x_{2022})$ moving clockwise around the circle. By convention, we define $x_i = x_j$ if $i \equiv j $ $(mod \ 2022)$. Define a function \[f(\mathcal{P}) = \sum_{i=1}^{2022} |x_i - x_{i+1}|\] For some permutation $\mathcal{P}$ of $(x_1, x_2, \dots, x_{2022})$. Let $f_{\max}$ and $f_{\min}$ be the maximimum and minimum values of $f$, respectively, over all permutations $\mathcal{P}$. Determine \[f_{\max} - f_{\min}\]

Problem 97B. Proposed by Max Jiang
Anthony the Ant likes crawling on Platonic solids. He always starts on a vertex of a Platonic solid. Every second, he chooses one of the edges at the vertex uniformly at random and walks along it to the vertex on the other side. Find the probability that the first time he comes back to the first vertex is after an even number of seconds if he is crawling on a: (i) Tetrahedron, (ii) Cube, or (iii) Dodecahedron.

Problem 98B. Proposed by Daisy Sheng
Let $c$ be an integer constant, where $c\geq 2$. Given that $x,y,w,z \in \mathbb{N}^+$ and $$(c+1)(ywz+2y+101z) = c(xywz+2xy+101xz+wz+2),$$ find all possible values of $x+y+w+z$ in terms of $c$.

Problem 99B. Proposed by Vedaant Srivastava
Arrange the numbers from 1 to 2022 in a circle. Label the numbers $(x_1, x_2, \dots, x_{2022})$ moving clockwise around the circle. By convention, we define $x_i = x_j$ if $i \equiv j $ $(mod \ 2022)$. Define a function \[g(\mathcal{P}) = \sum_{i=1}^{2022} x_i \cdot x_{i+1}\] For each permutation $\mathcal{P}$ of $(x_1, x_2, \dots, x_{2022})$. Determine the maximum of $g(\mathcal{P})$ over all permutations $\mathcal{P}$.