Issue #4 - January 20, 2021

Problems A (Not open to Grade 11 and 12 students)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Saturday, February 20, 2021 to submit solutions.

Problem 27A. Proposed by DC
In any triangle ABC, find the ratio $$\frac{sinA+sinB+sinC}{cotA+cotB+cotC}$$ function of the altitudes ($h_A,h_B,h_C$) in the triangle.

Problem 28A. Proposed by Max Jiang
The number 2021 is written on a blackboard. Alice and Bob play a game where they take turns erasing the current number on the blackboard, $n$, and write either $n-1$ or $n-336$. They cannot write negative integers and the player who writes 0 is the winner. Given that Alice goes first, show that Alice has a winning strategy.

Problem 29A. Proposed by Vedaant Srivastava
At the annual Obscure Meeting for Journalists, there are to be 2021 journalists seated around a circular table. Each journalist is assigned a number from 1 to 2021 depending on their political polarization. For each pair of journalists sitting next to one another, their disagreement is defined as the absolute difference between their assigned numbers. The disagreement index for a given table arrangement is the sum of the disagreement of all adjacent journalists. Given that the journalists sit around the table uniformly at random, what is the expected value of the disagreement index?

Problem 30A. Proposed by Alexander Monteith-Pistor
Let $A_1B_1, A_2B_2, A_3B_3, A_4B_4$ be four line segments of length $10$. For each pair $1 \le i < j \le 4$, the line segments $A_iB_i$ and $A_jB_j$ intersect at point $P_{ij}$. Starting at $A_{1}$ and travelling along the four line segments, find the least upper bound for the distance one has to travel to pass through all $6$ points of intersection ($P_{12}$, $P_{13}$, $P_{14}$, $P_{23}$, $P_{24}$, $P_{34}$).

Problem 31A. Proposed by Andy Kim
Find the volume of a rectangular prism that has faces with diagonals of length 8, 10, and 12.

Problem 32A. Proposed by Nicholas Sullivan
The Riemann zeta function is defined $\zeta(n) = \sum_{k = 1}^{\infty} \frac{1}{k^n}$ and has lots of interesting properties. For example, the sum of inverse squares is equal to $\zeta(2) = \frac{\pi^2}{6}$. If we let $a_n = \zeta(n) - 1$, then show that: \begin{equation*} \sum_{n = 1}^{\infty} a_{2n} = 3 \sum_{n = 1}^{\infty} a_{2n+1}. \end{equation*}

Problem 33A. Proposed by DC
On a circle with diameter AB, take two points C and D and build the intersection between AC and BD denoted as P. Prove that $$BD^2-BC^2=AC\times PC+BD\times DP$$

Problem 34A. Proposed by DC
In triangle ABC with angle $A = 45$ degrees, build D, the projection of B on AC and E, the projection of C on AB. Find the ratio between the area of triangle ADE and area of triangle ABC.

Problem 35A. Proposed by DC
In trapezoid ABCD, the bases are AB=7 cm and CD=3 cm. The circle with the origin at A and radius AD intersects diagonal AC at M and N. Calculate the value of the product $CM \times CN$.

 

Problems B (Open to all Grades)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Saturday, February 20, 2021 to submit solutions.

Problem 29B. Proposed by David Andrei Anghel
There are $n$ fixed lines ($l_1, l_2, \ldots, l_n$) in a given plane, with $n$ an odd natural number greater then 1. $P_0$ is a moving point on the same plane. For each $i \in \{1, 2, \ldots, 2n\} $ define $P_i$ as the symmetric of $P_{i-1}$ with respect to line $l_i$ (the indices are considered modulo $n$). Show that vector $P_0P_{2n}$ does not depend on the position of $P_0$.

Problem 30B. Proposed by Max Jiang
Given a string of $a$'s and $b$'s, we can replace a substring using the following operations: \begin{align*} \underbrace{aaa\cdots a}_k\underbrace{b\cdots bbb}_k&\implies\underbrace{abab\cdots ab}_{2k}, \\ \underbrace{abab\cdots ab}_{2k}&\implies\underbrace{aaa\cdots a}_k\underbrace{b\cdots bbb}_k, \\ \underbrace{bbb\cdots b}_k\underbrace{a\cdots aaa}_k&\implies\underbrace{baba\cdots ba}_{2k}, \\ \underbrace{baba\cdots ba}_{2k}&\implies\underbrace{bbb\cdots b}_k\underbrace{a\cdots aaa}_k, \end{align*} where $k\in\mathbb{N}$. For example, the following operations are valid: \begin{align*} \underbrace{aabb}ababbbaababa&\implies abab\underbrace{abab}bbaababa \\ &\implies ababaabb\underbrace{bbaa}baba \\ &\implies ababaabbbaba\underbrace{baba} \\ &\implies ababaabbbababbaa. \end{align*} Given the string \[\underbrace{aaa\cdots a}_n\underbrace{bbb\cdots b}_n,\] find all strings that are attainable by repeatedly applying the four operations.

Problem 31B. Proposed by Vedaant Srivastava
The Organization of Mathematicians in Jeopardy is hosting a new years ping pong tournament! There are 2021 mathematicians taking part in the tournament, where each competitor plays against each other exactly once. In each game, there is one winner and one loser. Given competitors $x, y, z,$ we say that a triple-upset has happened if $x$ wins against $y$, $y$ wins against $z$, and $z$ wins against $x$. What is the maximum possible number of triple-upsets in the tournament?

Problem 32B. Proposed by Alexander Monteith-Pistor
An arithmetic sequence is called maximal in a set $S$ if each of its elements are distinct and in $S$, and it is not contained in a larger such arithmetic sequence. For example, $1, 2, 3, 4$ is maximal in $\{1, 2, 3, 4, 6\}$ while $1, 2, 3$ is not. Similarly, a geometric sequence is called maximal in a set $S$ if each of its elements are distinct and in $S$, and it is not contained in a larger such geometric sequence.
Let $n \ge 3$. Let $A$ be the smallest integer such that every set of $n$ positive integers has at most $A$ maximal arithmetic sequences. Let $G$ be the smallest integer such that every set of $n$ positive integers has at most $G$ maximal geometric sequences. Prove that $A = G$.

Problem 33B. Proposed by Andy Kim
Let $p(x)$ be a polynomial with nonnegative integer coefficients. Prove or disprove the following statement: it is possible to determine every coefficient of $p(x)$ by evaluating it at 2 values.

Problem 34B. Proposed by Nicholas Sullivan
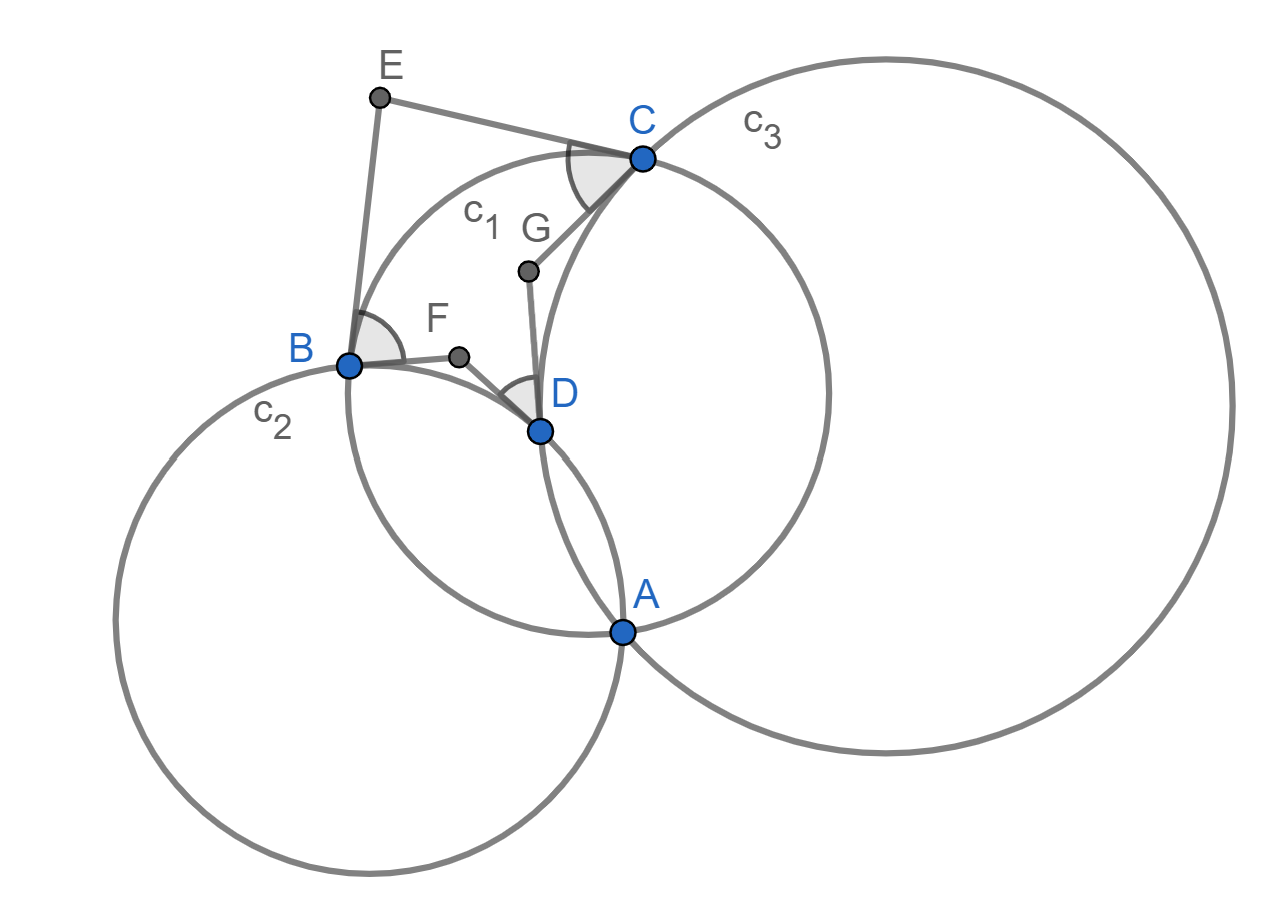
Let $A$, $B$, $C$ and $D$ be arbitrary points on the plane as seen in the figure below. Let $A$, $B$ and $C$ lie on circle $c_1$, let $A$, $B$ and $D$ lie on circle $c_2$ and let $A$, $C$ and $D$ lie on circle $c_3$. Let $E$ be the intersection of the tangents at $B$ and $C$ to circle $c_1$, let $F$ be the intersection of the tangents at $B$ and $D$ to circle $c_2$, and let $G$ be the intersection of the tangents at $C$ and $D$ to circle $c_3$, as in the figure. Show that $$ \mathrm{m}(\angle EBF) + \mathrm{m}(\angle FDG) + \mathrm{m}(\angle GCE) = 180\ degrees. $$

Problem 35B. Proposed by DC
Consider trapezoid $ABCD$ with $AD$=6 cm and $BC$=5 cm, and parallel sides $AB < CD$. If $E$ is the intersection of $AD$ with the circle on $BCD$ and $F$ is the intersection of $AD$ with the parallel from $C$ to $BE$, find the length of $EF$.

Problem 36B. Proposed by DC
Consider triangle $ABC$ with $AB=$ 5 cm and $BC=$ 6 cm. Build $AH$, the altitude and take point $P$ on $AH$ such that the circle with the origin at $P$ and radius $AP$ will intersect side $AB$ at $M$ and side $AC$ at $N$. Build a second circle on $M$ and $N$ that intersects side $AB$ at $R$ and side $AC$ at $S$. If $P$ and the second circle are built such that $AR=4$ cm, find $RS$.