Issue #5 - March 25, 2021

Problems A (Not open to Grade 11 and 12 students)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Thursday, April 29, 2021 to submit solutions.

Problem 30A. Proposed by Alexander Monteith-Pistor
Let $A_1B_1, A_2B_2, A_3B_3, A_4B_4$ be four line segments of length $10$. For each pair $1 \le i < j \le 4$, the line segments $A_iB_i$ and $A_jB_j$ intersect at point $P_{ij}$. Starting at $A_{1}$ and travelling along the four line segments, find the least upper bound for the distance one has to travel to pass through all $6$ points of intersection ($P_{12}$, $P_{13}$, $P_{14}$, $P_{23}$, $P_{24}$, $P_{34}$).

Problem 33A. Proposed by DC
On a circle with diameter AB, take two points C and D and build the intersection between AC and BD denoted as P. Prove that $$BD^2-BC^2=AC\times PC+BD\times DP$$

Problem 35A. Proposed by DC
In trapezoid ABCD, the bases are AB=7 cm and CD=3 cm. The circle with the origin at A and radius AD intersects diagonal AC at M and N. Calculate the value of the product $CM \times CN$.

Problem 36A. Proposed by Cosmina Ghitescu
Solve the equation $$10x^2+7=18x+11^y$$ where $x \in \mathbb{Z}$ and $y \in \mathbb{N}$.

Problem 37A. Proposed by Cosmina Ghitescu
Remark: The original submission was modified by AE.
Find all $x \in \mathbb{R}$ that satisfy the equation $$\left[ \frac{18x-4}{5} \right] + \left[ \frac{36x-3}{10} \right] = \frac{2(p-1)!+5}{p}$$ where $p$ is a prime number.

Problem 38A. Proposed by Cosmina Ghitescu
Remark: The original submission was modified by AE.
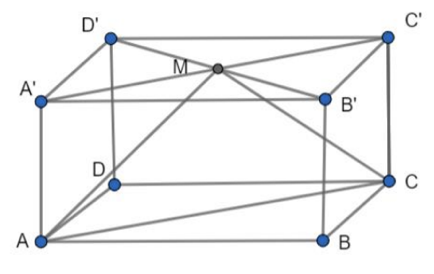Let $ABCDA'B'C'D'$ be a square-based prism with square faces $ABCD$ and $A'B'C'D'$. Let $AB = \sqrt{2} AA'$. Consider a point $M$ on the plane $(A'B'C'D')$ such that $\angle AMC \ge 90^{\circ}$.
Prove that :
(i) The measure of $\angle AMC$ can only be $90^{\circ}$;
(ii) $M$ is the center of the base $A'B'C'D'$.

Problem 39A. Proposed by Max Jiang
In a $2^n$-player single-elimination tournament, the players are seeded from 1 to $2^n$, where player $i$ will always win against player $j$ if $i< j$. In each round, the remaining players are paired up randomly. Find all pairs of players that are will be paired up at some point in the tournament no matter how the pairings are chosen each round.

Problem 40A. Proposed by Nicholas Sullivan
Let $a_0 = 1$, $a_1 = 1$ and $a_{n+1} = 2023a_n - a_{n-1}$, for all positive natural numbers $n$. Show that for all $n \geq 1$: \begin{equation*} \begin{split} a_{n+1}a_{n-1} - a_n^2 = 2021. \end{split} \end{equation*}

Problem 41A. Proposed by Alexander Monteith-Pistor
Find all functions $f : \mathbb{N} \to \mathbb{N}$ such that $f(1) = 1$ and $$f(p^km) = \sum_{i = 0}^{k-1} f(p^im)$$ for all $p, k, m \in \mathbb{N}$ where $p$ is a prime which does not divide $m$.

Problem 42A. Proposed by Vedaant Srivastava
Given positive reals $a, b, c$, prove that $$\frac{a(a^3+1)}{2b+6c} + \frac{b(b^3+1)}{2c+6a} + \frac{c(c^3+1)}{2a+6b} \ge \frac{1}{8}(a^3+b^3+c^3+3)$$

 

Problems B (Open to all Grades)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Thursday, April 29, 2021 to submit solutions.

Problem 37B. Proposed by Max Jiang
For an even integer $n$, find the number of ways to tile a $3\times n$ grid with dominoes in terms of $n$.

Problem 38B. Proposed by Nicholas Sullivan
Alice and Bob are playing a game called 'knights of the toroidal table' on a five-by-five square 'chessboard'. Each has a knight, which begin in opposite corners of the board. On each turn, the knight can move as a regular knight, that is, in an L-shape of two steps in one direction, and one step perpendicularly. However, if a knight goes over an edge, it reenters on the opposite side, as if the board were a torus.
Players make turns, and as soon as one player's knight is captured, or enters a square previously occupied by another knight, then this player loses the game, and the other player wins. If Alice moves first, who has the winning strategy, and what is it?

Problem 39B. Proposed by Alexander Monteith-Pistor
For $n \in \mathbb{N}$, let $S(n)$ and $P(n)$ denote the sum and product of the digits of $n$ (respectively). For how many $k \in \mathbb{N}$ do there exist positive integers $n_1, ..., n_k$ satisfying $$\sum_{i=1}^k n_i = 2021$$ $$\sum_{i=1}^k S(n_i) = \sum_{i=1}^k P(n_i)$$

Problem 40B. Proposed by Vedaant Srivastava
Two identical rows of numbers are written on a chalkboard, each comprised of the natural numbers from 1 to $10!$ inclusive. Determine the number of ways to pick one number from each row such that the product of the two numbers is divisible by $10!$

Problem 41B. Proposed by Nikola Milijevic
The positive integers \(a_1, a_2, \dots, a_n\) are not greater than 2021, with the property that lcm\((a_i,a_j)\) $>$ 2021 for all \(i, j, i \neq j \). Show that: \[ \sum_{i=1}^{n} \frac{1}{a_i} < 2 \]

Problem 42B. Proposed by Andy Kim
Define an $L$-region of size $n$ as an $L$-shaped region with two sides of length $2n$ and four sides of length $n$, and define an $L$-tile to be a tile with the same shape as an $L$-region of size 1 (i.e. a $2 \times 2$ square with one $1 \times 1$ square missing). Prove that an $L$-region of size $n$ can be tiled with $L$-tiles for all positive integers $n$.

Problem 43B. Proposed by Andy Kim
For $n \in Z^+ \cup \{0\}$, let $[[n]] = \{i \in Z \,|\, 1 \leq i \leq n\}$. Also, for a set of positive integers $A$, let $S(A)$ be the sum of the elements of $A$. Find (and prove) a formula for $$\sum_{A\subseteq [[n]]} \sum_{B\subseteq [[n]]} S(A \cup B)$$

Problem 44B. Proposed by DC
Consider triangle ABC with $\angle ABC = 30^{\circ}$ and $\angle ACB = 15^{\circ}$ and M the midpoint of the side BC. Build AN, the angle bisector of $\angle MAC$, with N on BC. Calculate the ratio $\frac{NC}{AB}$.

Problem 45B. Proposed by DC
In triangle ABC with $\angle B = 30^{\circ}$ prove that $sin(A) +cos(C) \leq \sqrt{3}$.