Issue #6 - May 19, 2021

Problems A (Not open to Grade 11 and 12 students)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Friday, June 18, 2021 to submit solutions.

Problem 35A. Proposed by DC
In trapezoid $ABCD$, the bases are $AB$=7 cm and $CD$=3 cm. The circle with the origin at $A$ and radius $AD$ intersects diagonal $AC$ at $M$ and $N$. Calculate the value of the product $CM \times CN$.

Problem 41A. Proposed by Alexander Monteith-Pistor
Find all functions $f : \mathbb{N} \to \mathbb{N}$ such that $f(1) = 1$ and $$f(p^km) = \sum_{i = 0}^{k-1} f(p^im)$$ for all $p, k, m \in \mathbb{N}$ where $p$ is a prime which does not divide $m$.

Problem 42A. Proposed by Vedaant Srivastava
Given positive reals $a, b, c$, prove that $$\frac{a(a^3+1)}{2b+6c} + \frac{b(b^3+1)}{2c+6a} + \frac{c(c^3+1)}{2a+6b} \ge \frac{1}{8}(a^3+b^3+c^3+3).$$

Problem 43A. Proposed by Alexandru Benescu
Let $ABCDA'B'C'D'$ be a cube , $R$ the midpoint of $BB'$, $S$ the midpoint of $AD$ and $T$ on $C'D'$, such that $\frac{C'T}{D'T}=2$. Find $cos(\angle SC, TR)$.

Problem 44A. Proposed by Gabriel Crisan
Let us consider the sum: $$S_n=\frac{3}{1!+2!+3!}+\frac{4}{2!+3!+4!}+\cdots+\frac{n+2}{n!+(n+1)!+(n+2)!}.$$ Solve the equation: $$4x=\left[\frac{11}{2}+S_{10}\right]-x^2,$$ where $[y]$ is the floor of $y \in \mathbb{R} $.

Problem 45A. Proposed by Alexandru Benescu
Let $a$ and $b$ be positive real numbers such that $a(a+2b-2)=8b(b+1)$. Find the value of $\frac{a}{b+1}$.

Problem 46A. Proposed by Alexandru Benescu
Let $a$, $b$ and $c$ be positive real numbers such that $abc(a+b+c) \geq a^2+b^2+c^2$. Find the minimum of the expression $a^2+b^2+c^2$.

Problem 47A. Proposed by Max Jiang
Find all integer solutions $(a,b,c)\in\mathbb{Z}^3$ for \[1+\frac{3}{b}+\frac{2}{c}+\frac{6}{bc}=\frac{1}{a}+\frac{3}{ab}+\frac{2}{ac}+\frac{25}{abc}.\]

Problem 48A. Proposed by Vedaant Srivastava
Let $G$ be the set of all lattice points $(x, y)$ on the Cartesian plane where $0 \le x, y \le 2021$. Suppose that there are $2022$ roadblocks positioned at points in $G$ such that no two roadblocks have the same $x$ or $y$ coordinate. Anna starts at the point $(0, 0)$, attempting to reach the point $(2021, 2021)$ through a sequence of moves. In each move, she moves one unit up, down, left, or right, such that she always remains in $G$. Given that Anna cannot visit a lattice point which is occupied by a roadblock, determine all configurations of the roadblocks in which Anna is unable to reach her destination.

Problem 49A. Proposed by Alexander Monteith-Pistor
Let $T_1$ and $T_2$ be triangles. We write $T_1 \hookrightarrow T_2$ if the interior of $T_2$ can be divided into triangles, all of which are similar to $T_1$. Prove that there exists an infinite set of triangles $S$ such that, for any distinct $T, T' \in S$, $T \hookrightarrow T'$ is false.

Problem 50A. Proposed by Nicholas Sullivan
Let $O$ be the intersection point of the two diagonals of non-degenerate quadrilateral $ABCD$. Next, let $E$, $F$, $G$ and $H$ be the midpoints of $AB$, $BC$, $CD$ and $DA$ respectively. If $EG$ and $FH$ intersect at $O$, show that $ABCD$ is a parallelogram.

Problem 51A. Proposed by Andy Kim
Let $a,b,c$ be positive reals. Prove $$\frac{a^2}{b} + \frac{b^2}{c} + \frac{c^2}{a} \geq a + b + c.$$

Problem 52A. Proposed by Andy Kim
Let $n$ be a positive integer, and let $$a_n = 1 \cdot {n \choose 1} + \dots + n \cdot {n \choose n} = \sum_{i = 1}^{n} i \cdot {n \choose i}$$ $a)$ Prove that $a_n$ is divisible by $n$.
$b)$ Find a value for $a_n$ in terms of $n$.

Problem 53A. Proposed by Nikola Milijevic
The positive integers \(a_1, a_2, \dots, a_n\) are not greater than 2021, with the property that lcm\((a_i,a_j)\) $>$ 2021 for all \(i, j, i \neq j \). Show that: \[ \sum_{i=1}^{n} \frac{1}{a_i} < 2 \]

 

Problems B (Open to all Grades)

Note 1: Problems are not in order of difficulty.
Note 2: You will have until midnight on Friday, June 18, 2021 to submit solutions.

Problem 39B. Proposed by Alexander Monteith-Pistor
For $n \in \mathbb{N}$, let $S(n)$ and $P(n)$ denote the sum and product of the digits of $n$ (respectively). For how many $k \in \mathbb{N}$ do there exist positive integers $n_1, ..., n_k$ satisfying $$\sum_{i=1}^k n_i = 2021$$ $$\sum_{i=1}^k S(n_i) = \sum_{i=1}^k P(n_i)$$

Problem 40B. Proposed by Vedaant Srivastava
Two identical rows of numbers are written on a chalkboard, each comprised of the natural numbers from 1 to $10!$ inclusive. Determine the number of ways to pick one number from each row such that the product of the two numbers is divisible by $10!$

Problem 42B. Proposed by Andy Kim
Define an $L$-region of size $n$ as an $L$-shaped region with two sides of length $2n$ and four sides of length $n$, and define an $L$-tile to be a tile with the same shape as an $L$-region of size 1 (i.e. a $2 \times 2$ square with one $1 \times 1$ square missing). Prove that an $L$-region of size $n$ can be tiled with $L$-tiles for all positive integers $n$.

Problem 46B. Proposed by Ana Maria Popa
For positive numbers $x$, $y$, and $z$ show that: $$S=\frac{(x+z-y)^2}{4}+ \frac{(x+y-z)^2}{4}+\frac{(y+z-x)^2}{4}+\frac{(x+z-y)^2}{4y^4}+$$ $$+\frac{(x+y-z)^2}{4z^4}+\frac{(y+z-x)^2}{4x^4}\geq \frac{3}{2}.$$

Problem 47B. Proposed by Andrei Radu Vasile
Given $a$, $b$, $c$ positive real numbers such that $a+b+c=15$, prove that: $$\frac{a}{a^2+50}+\frac{b}{b^2+50}+\frac{c}{c^2+50}\leq\frac{1}{5}.$$

Problem 48B. Proposed by Alexandru Benescu
Let $x$ and $p$ be positive integers with $p$ prime, such that: $$x^{x^{x^{{\cdots}^x}}}=p^{p^{p^{{\cdots}^p}}},$$ where $x$ appears $p$ times and $p$ appears $x$ times. Prove that $x^2+p^2+2(x-p-xp)$ is nonnegative.

Problem 49B. Proposed by Cosmina Ghitescu
Solve the equation $2021+2^x=7^y5^z$, where $x$,$y$,$z \in \mathbb{N}$.

Problem 50B. Proposed by Cosmina Ghitescu
Let $a$, $b$, $c$ be the lengths of the sides of a triangle and $a$, $b$, $c \in \mathbb{Q_{+}}$, such that they verify the system: \[\left\{\begin{array}{c}\frac{a}{b}+c=\frac{4(a+bc)}{(b+1)^2}\\ \frac{a+c}{b+1}+\sqrt{ac}=\frac{7+4\sqrt{3}}{10}\end{array}\right.\] Find the area of the triangle.

Problem 51B. Proposed by Cosmina Ghitescu
Find the minimum of the expression $$E=\frac{1-cos^2A}{2cosA+cos^2A+1}+\frac{1-cos^2B}{2cosB+cos^2B+1}+\frac{1-cos^2C}{2cosC+cos^2C+1},$$ where $A$,$B$, and $C$ are the angles of a triangle.

Problem 52B. Proposed by Daisy Sheng
Find the general form for the integer $k$ such that the expression $$2^{n+1}+5^{n+2}\cdot3^{2n+4}\cdot k + (2k+1)\cdot (47 \cdot 3)^{n+3}$$ is divisible by 2021 for all positive integers $n$ that are odd multiples of $3$. For reference, $2021 = 43 \cdot 47$.

Problem 53B. Proposed by Daisy Sheng
Quadrilateral $ABCD$ is constructed with $M$ as the midpoint of $AD$ and $2AB>AD$. Let the circumcircle of triangle $ACD$ intersect $AB$ at $K$ and $BD$ at $N$, where arc $KN=30^{\circ}$ and $ \angle ABD = 45^{\circ}$ (see figure below). If $CD^2 + 2AC\cdot AB = 4AB^2 + AC \cdot CD$ and $\cos(m(\angle BAD))=\frac{AB-AC}{AD}$, prove that $BM=CM$.
Note: Inspired by a TST Problem for Girls' Math Team Canada.

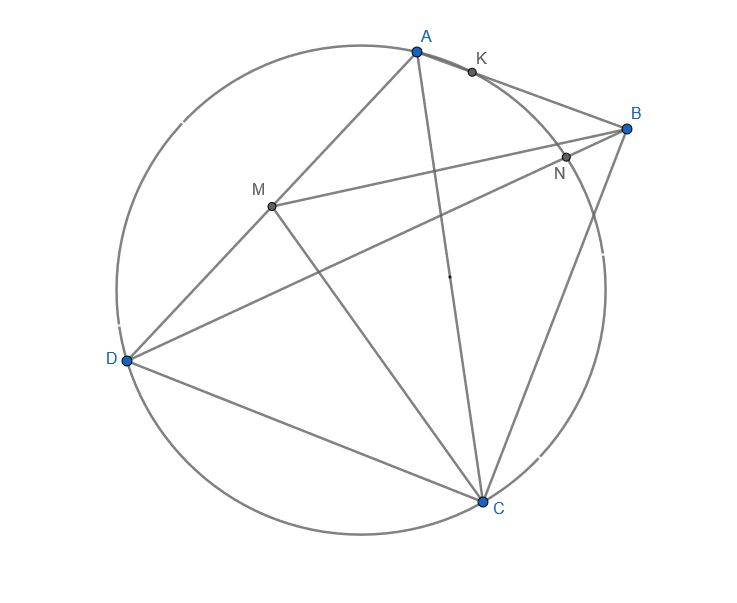
Problem 54B. Proposed by Max Jiang
Find all functions $f:\mathbb{R}\to\mathbb{R}$ that satisfy the following property: Given an ordered pair $(x,y)\in\mathbb{R}^2$, we have either \begin{align*} f(x)-f(y)&=f(x^2-y^2) \\ f(x)f(y)&=f(x^2y^2) \end{align*} or \begin{align*} f(y)&\ne0 \\ f(x)+f(y)&=f(x^2-y^2) \\ f(x)/f(y)&=f(x^2y^2). \end{align*} Note: it is possible that an ordered pair $(x,y),x\ne y$ satisfies the first set of conditions while the ordered pair $(y,x)$ satisfies the other set.

Problem 55B. Proposed by Vedaant Srivastava
Determine all functions $f : \mathbb{Q} \to \mathbb{Q}$ such that $$2f(x+y) + 2f(x-y) = f(2x) + f(2y)$$ for all $x, y \in \mathbb{Q}$.

Problem 56B. Proposed by Alexander Monteith-Pistor
A game is played with white and black pieces and a chessboard ($8$ by $8$). There is an unlimited number of identical black pieces and identical white pieces. To obtain a starting position, any number of black pieces are placed on one half of the board and any number of white pieces are placed on the other half (at most one piece per square). A piece is called matched if its color is the same of the square it is on. If a piece is not matched then it is mismatched. How many starting positions satisfy the following condition $$ # of matched pieces -# of mismatched pieces = 16$$ (your answer should be a binomial coefficient).

Problem 57B. Proposed by Nicholas Sullivan
Consider two perpendicular vectors $\mathbf{a}, \mathbf{b}$ in $\mathbb{R}^3$. If these vectors have components $\mathbf{a} = (\sin\alpha, \sin\beta, \sin\gamma)$ and $\mathbf{b} = (\cos\alpha, \cos\beta, \cos\gamma)$ respectively, and \begin{equation*} \begin{split} \sin^2(\alpha - \beta) + \sin^2(\beta - \gamma) + \sin^2(\gamma - \alpha) & = 2, \end{split} \end{equation*} then find $|\mathbf{a}|^4 + |\mathbf{b}|^4$.